随着2020年ChatGPT3的发布,人工智能迎来了快速的发展,此后,国内外各种大模型如雨后春笋般快速发展。
当然,本文将不会探究大模型的过多技术细节,了解「神经网络」能够更好地让我们理解大模型,所以本文仅仅从入门的角度上,谈谈作为人工智能底层技术的「神经网络」是什么?为什么可以有这么大的能量?
世界的本质-函数
这个问题有点偏哲学,但是放在今天讨论的话题上来看,再合适不过了。先说结论,在人工智能的世界里,我们可以说世界本质是函数。
示例1:当一个物体从高处做自由落体时,下落的高度$h$可以是关于$t$的函数,我们知道可以表示为:
$$h = \frac{1}{2}gt^2$$
示例2:一个浸在流体中的物体所受到竖直向上的浮力,其大小等于物体所排开流体的重力,用公式可以表示为: $$F_{浮力}=ρ_{液}gv_{排开流体}$$
通过这两个例子,我们发现,人类对这个世界的理解,就是通过函数的方式来描述世界的规律。基于这个结论,我们大胆假设,如果世间万物都有一个与时间$t$的函数关系,是不是我们就可以预测未来呢?
既然真实世界,我们可以将规律抽象成一个函数来描述,那么用计算机来解决问题是不是也可以定义为如何抽象成一个函数呢?
最小二乘法问题
在高中时,我们曾经学习过最小二乘法,来解决线性回归问题,线性回归问题也可以称为一种预测算法,通过历史数据来预测未知数据。
问题描述为:假设有一组数据,我们希望求出对应的一元线性模型来拟合这一组数据的映射关系: $$y = β_{0} + β_{1}x$$
同时,我们也知道,$β_{0}$和$β_{1}$对应的求解公式(有兴趣的话,可以看下推导过程:最小二乘法的推导证明:
$$β_{0}=\bar{y}-β_{1}\bar{x}$$ $$β_{1}=\frac{\sum_{i=1}^m(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^m(x_i-\bar{x})^2}$$
假如有这么一组数据:(25, 110), (27, 115), (31, 155), (33, 160), (35, 180),请根据这些数据,预测当x=40时,对应的y值:
通过上面的公式,我们推导出,线性方程为:$y = 7.2x - 73.7$
于是,我们可以预测当x=40时,$y=214.3$
恭喜你,读到这里,其实你已经学会了神经网络的本质,能够通过现有的数据拟合一个函数,然后通过拟合的函数预测数据。而计算$β_{0}$和$β_{1}$的过程就是训练过程。
但是现实世界中的问题是很复杂的,并不总是线性的,而且我们也没有办法确定一个函数关系,例如是线性的,还是二次?所以我们需要一个通用的算法,能够根据我们提供的数据自动拟合一个函数关系。如果存在这种能力,我们就可以描述这个世界的一些规律。为了解决这个问题,提出了神经网络的理论。下面我们将分析神经网络是如何来解决我们的问题。
神经网络
神经网络是一种机器学习模型,它以类似于人脑的方式做出决策,通过使用模仿生物神经元协同工作方式的过程来识别现象、权衡利弊并得出结论。
每个神经网络都由多个节点层或人工神经元组成 – 一个输入层、一个或多个隐藏层和一个输出层。每个节点都与其他节点相连,具有一个关联的权重和阈值。如果任何单个节点的输出高于指定的阈值,那么该节点将被激活,并将数据发送到网络的下一层。否则,不会将数据传递到网络的下一层。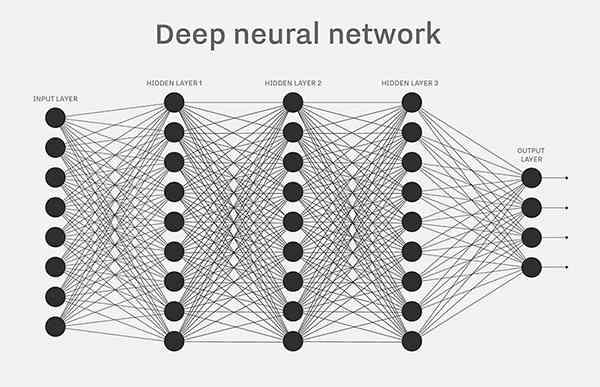
神经元
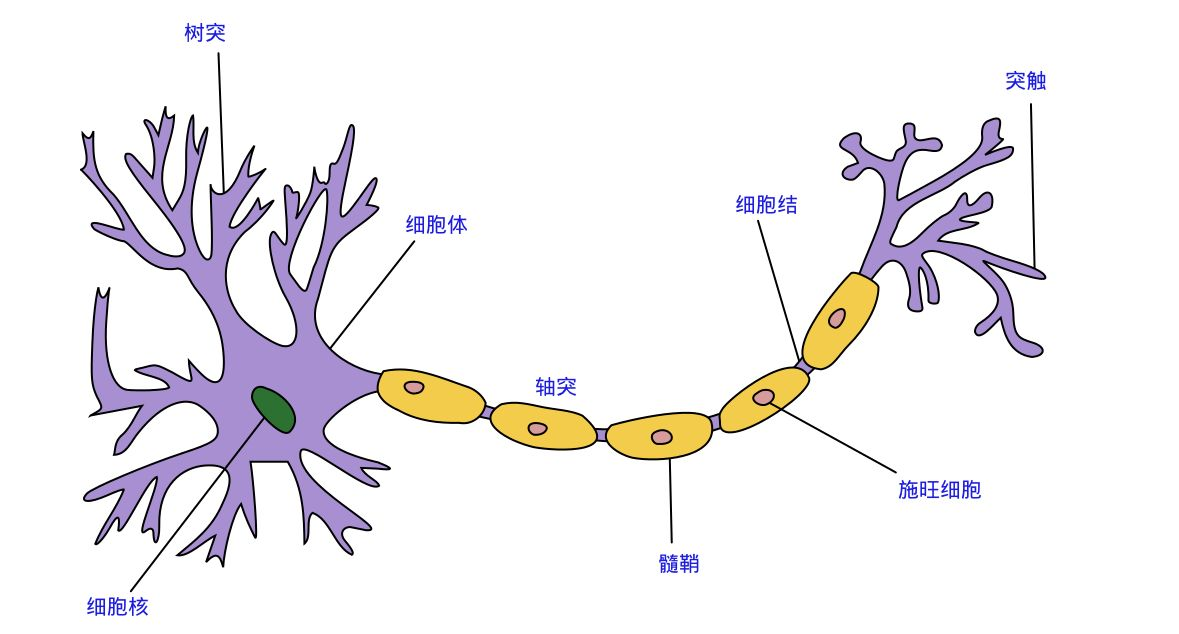
提出神经网络之初,就是为了模拟人为的思考方式,所以基于人的神经元模型,人为也构造了类似的“人工神经元”模型。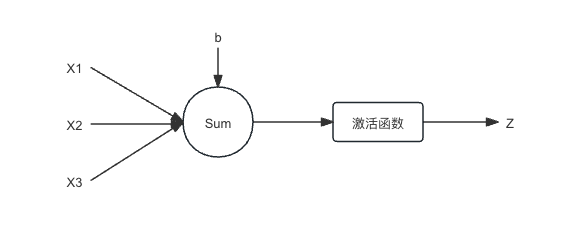
通过上图,我们可以通过数学公式来描述一个神经元的计算逻辑: $$Z=g(\sum_{i=0}^{n}(x_{i}*w_{i})+b)$$
激活函数
从上一章节,我们发现,在神经元内部进行加权求和之后,又会经过一个激活函数处理,这个激活函数有什么作用呢?
我们假设,没有这个激活函数,并且这个神经网络有三层:输入层、隐藏层、输出层。 那么我们就知道,输入层到隐藏层的结果为:
$$Z_1 = \sum_{i=0}^{n}(x_{i}*w_{i})+b$$
换成向量表示: $$Z_1 = X*W_1^T+b$$
同理我们可以计算出,隐藏层到输出层的结果为: $$Z_2 = Z_1*W_2^T+b$$
因为$Z_1$和$Z_2$都是线性方程,所以本质上是可以用一个现场方程来表示的,也就是说这个神经网络不管有几层都没有意义,因为都能通过一层来表示。
所以为了解决这个问题,我们就得在每一层后面加一个非线性变换,这样,相邻的两层无法等价于一层。
还有一个原因,引入非线性的激活函数可以增强神经网络的表达。
比如,对于一个二分类问题,不管增加多少层,神经网络只能使用直线来分隔,而引入非线性变换是会变直为曲。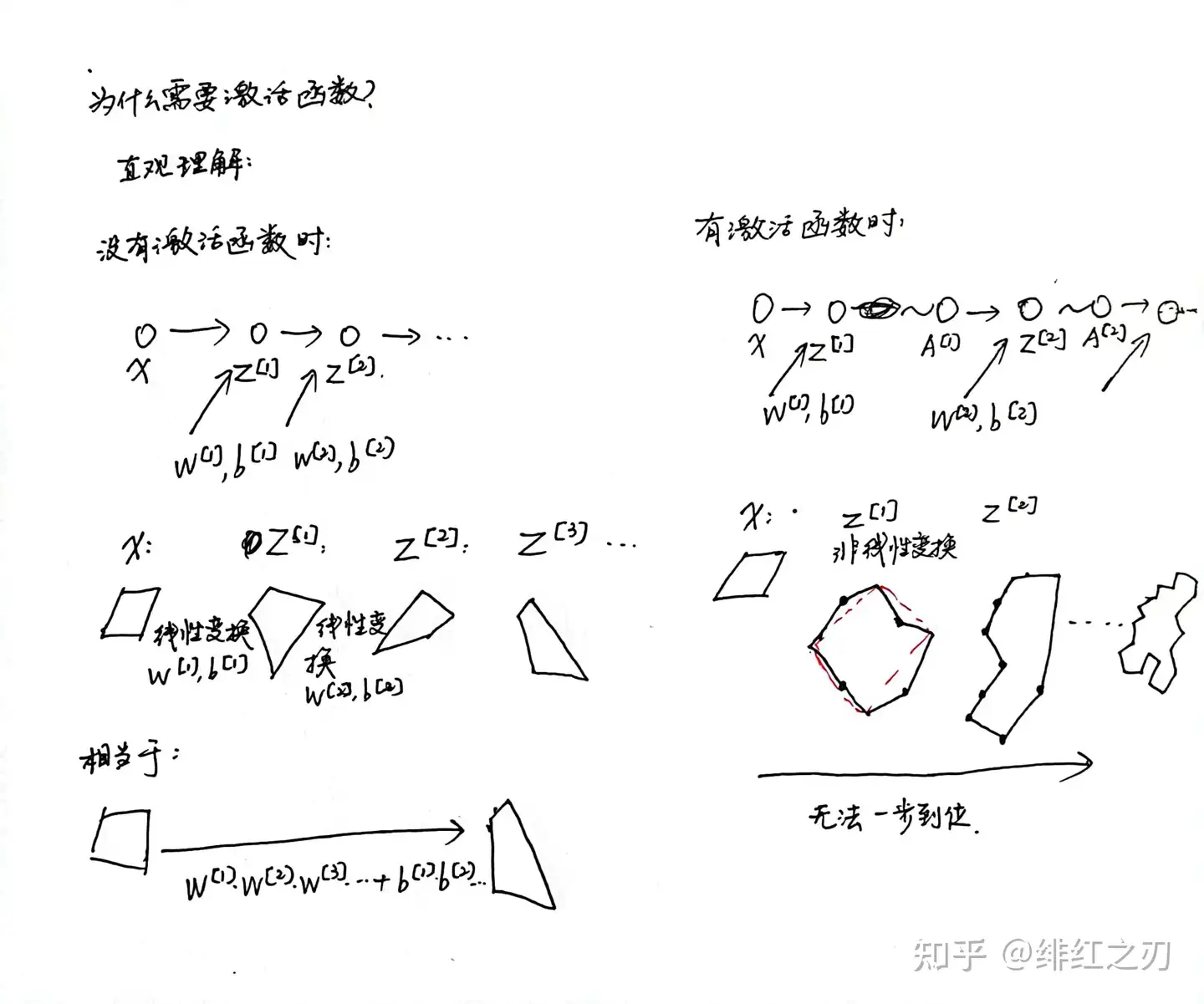
为什么是神经网络
上文,我们简单聊了一下神经网络的基本概念,以及如何来实现的。现在我们需要问一个问题,为什么神经网络能够解决实际中的问题?在第一章,我们给出了一个很具有哲学性的结论:世界的本质是函数。如果神经网络能够解决实际中的问题,那就应该具备能够将世间万物拟合成一个函数的能力。
在人工神经网络的数学理论中, 通用近似定理(或称万能近似定理)指出人工神经网络近似任意函数的能力。 苏联数学家安德烈·柯尔莫哥洛夫与学生弗拉基米尔·阿诺尔德在1950年代及60年代期间,证明多元函数可分解为以下形式: $$f(x_1,…x_n) = \sum_{q=0}^{2n}χ_q(\sum_{p=1}^nψ^{pq}(x_p))$$ 任意n元连续函数$f(x_1,…x_n)$都可以用一元连续函数的叠加来表示。即:对于任意整数$n>2$,存在定义在区间$[0,1]$上的连续单调增实值函数$ψ^{pq}(x)(p=1,2,…,n;q=1,2,…,2n+1)$,使得$E^n$中的任意连续函数$f(x_1,…x_n)$都可以写成上述的表达
换句话说:任意多元的连续函数可以表示为有限个二元连续函数的叠加。神经网络理论上就是构造多个二元连续函数叠加来实现的,所以也就证明了理论上神经网络是可以拟合任意的函数。
单层神经网络
1957年 Frank Rosenblatt 提出了一种简单的人工神经网络,被称之为感知机。由一个输入层和一个输出层构成,因此也被称为“单层感知机”。感知机的输入层负责接收实数值的输入向量,不做计算,输出层里的“输出单元”则需要对前面一层的输入进行计算。由于其结构特点,感知器只能作为一种线性分类模型,而不能完成非线性分类。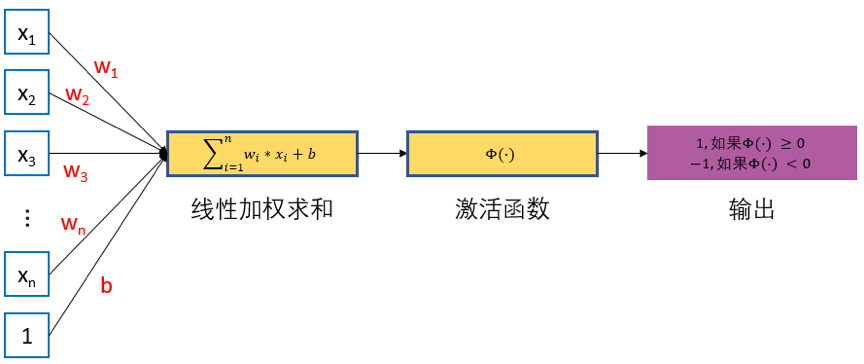
从结构上来看,感知器(单层神经网络)和神经元有点相似,但是也有一些差异性:
- 神经元的输入为其他神经元的输出信号,而感知器的输入为一层神经元。
- 感知器的激活函数是$sign$函数,而神经元的激活函数没有要求。
- 感知器可以采用有监督的方式学习到参数值,而神经元模型的参数是不能被学习的。
感知机的模型也可以被简单表示为: $$f(x) = sign(W^T*X + b)$$
正如上面所说,感知机的激活函数为$sign$函数,其表达式为: $$ sign(x) = \begin{cases} +1, & x\ge 0 \\ -1, & x< 0 \end{cases} $$
限制
单层神经网络对线性二分类问题很有用,但是无法解决非线性问题。本质上,单层神经网络是通过一条直线将平面分成两部分,而平面元素的点按照分布可能存在以下四种情况:
换句话说,对于XOR问题中的4个点(0,0), (0,1), (1,0), (1,1)无法找到一条直线 $w_1x_1+w_2x_2=b=0$能够将(0,1), (1,0)和(0,0), (1,1)分为一组。
为了解决感知机的这个问题,我们需要引入更复杂的神经网络,例如多层感知机,它含有隐藏层和非线性激活函数,能够处理非线性问题。
两层神经网络
从上文我们知道,单层神经网络是无法解决异或问题的,但是当增加一个计算层以后,两层神经网络不仅可以解决异或问题,而且具有非常好的非线性分类效果。我们知道在神经网络中,权重参数都是靠训练过程中计算出来的,多增加了一层之后,也就带来了复杂的计算问题。
1986年,Rumelhar和Hinton等人提出了反向传播(Backpropagation,BP)算法,解决了两层神经网络所需要的复杂计算量问题,从而带动了业界使用两层神经网络研究的热潮。
现在我们使用一些标记来区分不同层次之间的变量。
$w_{j,k}^l$:代表第$l$层第$j$个神经元与下一层第$k$个神经元之间的权重。
$a_j^l$:表示第$l$层第$j$个神经元的输出。
$z_j^l$:表示第$l$层第$j$个神经元的输入。
$b_j^l$:表示第$l$层第$j$个神经元的偏置。
前向传播
我们先定义下什么是前向传播:按顺序(从输入层到输出层)计算和存储神经网络中每层的结果。其实在前面介绍单层神经网络过程中,我们已经给过前向传播的计算,只是没有给出定义。
下面,我们来用代数形式来表达一下前向传播过程:
中间层的计算:
$$ \begin{cases} a_1^2=g(a_1^1 * w_{1,1}^1+a_2^1 * w_{2,1}^1+b_1^2)\\ a_2^2=g(a_1^1 * w_{1,2}^1+a_2^1 * w_{2,2}^1+b_2^2) \end{cases} $$
输出层计算: $$a_1^3=g(a_1^2 * w_{1,1}^2+a_2^2*w_{2,2}^1 + b_1^3)$$
将上面的表达式转换成矩阵表示: $$ \begin{cases} A^2=g(W^1 * A^1+B^2)\\ A^3=g(W^2 * A^2+B^3) \end{cases} $$ 其中$A^l$代表第$l$层的输出矩阵,$W^l$代表第$l$层与下一层的权重矩阵,$B^l$代表第$l$层的偏置矩阵
反向传播
前面我们说过,神经网络中的参数,就是在训练过程中,自动计算出来的。而反向传播就是用于训练这些参数的算法,它是一种通过计算梯度来更新网络参数的有效方法,以使网络能够逐步学习和调整权重。
从之前的分析中,我们知道,其实神经网络的本质就是拟合函数。那么衡量一个神经网络的好坏就是判断拟合的函数是否能够表达需要训练的规律。而训练过程就是降低预测输出与真实输出的差距,而这个差距一般是通过损失函数来表达,而我们要做的就是将这个损失函数的值降低足够低,最好是$0$。
损失函数我们一般表示为:
$$C=\frac{1}{2}||y-a^L||^2=\frac{1}{2}\sum_{j=1}^{K}(a_j^L-y_j)^2$$
其中$\frac{1}{2}$为系数,为了求导之后约掉简化计算。$y$为真实的输出。
从上面的推导,我们知道,$C$的值本质上只和权重$W$和偏置$B$有关。那么问题就变成了,我们通过不断迭代训练更新$W$和$B$的值来使得$C$最小。
而优化过程中,我们常常使用的数学工具就是梯度下降算法,这里因为不是我们讨论的重点,我们只是使用即可:
$$\theta^1=\theta^0-\alpha \bigtriangledown J(\theta)$$
$J$是关于$\theta$的一个函数,我们当前所处的位置为$\theta^0$点,要从这个点走到$J$的最小值点。首先我们先确定前进的方向,也就是梯度的反向,然后走一段距离的步长,也就是$\alpha$,走完这个段步长,就到达了$\theta^1$这个点!
下面,我们从输出层开始进行推导。
输出层->隐藏层 假设更新后的$b^3$仍然还是$b^3$,根据上文说的梯度下降算法,所以就有: $$b^3=b^3-\eta \frac{\partial C}{\partial b^3}$$
所以我们只需要求出损失函数和偏置值$b^3$的偏导即可。 从上面的定义,我们可以得出:
$$ \begin{align*} C&=\frac{1}{2}(a_1^3-y)^2 \\ &=\frac{1}{2}(g(a_1^2 * w_{1,1}^2+a_2^2 * w_{2,1}^2 + b_1^3)-y)^2\ \end{align*} $$
求出损失函数$C$对偏置$b_1^3$的偏导 $$ \begin{align*} \frac{\partial C}{\partial b_1^3} &= \frac{\partial C}{\partial a_1^3} * \frac{\partial a_1^3}{\partial b_1^3} \\ &= \frac{\partial C}{\partial a_1^3} * \frac{\partial a_1^3}{\partial z_1^3} * \frac{\partial z_1^3}{\partial b_1^3}\\ &=(a_1^3-y) * a_1^3*(1-a_1^3)&(a_1^3=g(z_1^3)) \end{align*} $$
代入梯度下降公式: $$b_1^3=b_1^3-\eta ((a_1^3-y) * a_1^3*(1-a_1^3))$$
同理,可以通过求出损失函数$C$对权重$w_{1,1}^2$和$w_{2,1}^2$的偏导,来计算权重的梯度。 $$ \begin{align*} \frac{\partial C}{\partial w_{1,1}^2} &= \frac{\partial C}{\partial a_1^3} * \frac{\partial a_1^3}{\partial z_1^3} * \frac{\partial z_1^3}{\partial w_{1,1}^2} \\ &= (a_1^3-y)a_1^3(1-a_1^3)a_1^2 \end{align} $$
$$ \begin{align*} \frac{\partial C}{\partial w_{2,1}^2} &= \frac{\partial C}{\partial a_1^3} * \frac{\partial a_1^3}{\partial z_1^3} * \frac{\partial z_1^3}{\partial w_{2,1}^2} \\ &= (a_1^3-y)a_1^3(1-a_1^3)a_2^2 \end{align} $$
导入梯度下降公式可得: $$w_{1,1}^2=w_{1,1}^2-\eta (a_1^3-y)a_1^3(1-a_1^3)*a_1^2$$ $$w_{2,1}^2=w_{1,1}^2-\eta (a_1^3-y)a_1^3(1-a_1^3)*a_2^2$$
至此,我们计算出了所有输出层->隐藏层的所有反向传播权重和偏置($w_{1,1}^2$ $w_{2,1}^2$ $b_1^3$)。
隐藏层->输入层 按照上面的思路,为了求$b_1^2$的参数变换,我们需要求出损失函数$C$对$b_1^2$的偏导。 为了再求偏导时,各个变量的关系更清楚,我们在这里再写出他们的关系。
$$ \begin{align*} a_1^3&=g(z_1^3) \\ z_1^3&=a_1^2 * w_{1,1}^2 + a_2^2 * w_{2,1}^2 + b_1^3 \\ a_1^2&=g(z_1^2) \\ z_1^2&=a_1^1 * w_{1,1}^1 + a_2^1 * w_{2,1}^1 + b_1^2 \end{align*} $$
$$ \begin{align*} \frac{\partial C}{\partial b_1^2} &= \frac{\partial C}{\partial a_1^3} * \frac{\partial a_1^3}{\partial z_1^3} * \frac{\partial z_1^3}{\partial a_1^2} * \frac{\partial a_1^2}{\partial z_1^2} * \frac{\partial z_1^2}{\partial b_1^2}\\ &=(a_1^3-y) * a_1^3*(1-a_1^3) \end{align*} $$
